Thermodynamics
Thermodynamics is a branch of physics which deals with the energy and work of a system.
It is useful, at this stage, to make a distinction between the different sizes of the systems that we are going to examine. We shall call a system microscopic if it is roughly of atomic dimensions, or smaller. On the other hand, we shall call a system macroscopic when it is large enough to be visible in the ordinary sense.
Energy transfer is studied in three types of systems:
Open systems Open systems can exchange both matter and energy with an outside system. They are portions of larger systems and in intimate contact with the larger system. Your body is an open system.
Closed systems Closed systems exchange energy but not matter with an outside system. Though they are typically portions of larger systems, they are not in complete contact. The Earth is essentially a closed system; it obtains lots of energy from the Sun but the exchange of matter with the outside is almost zero.
Isolated systems Isolated systems can exchange neither energy nor matter with an outside system. While they may be portions of larger systems, they do not communicate with the outside in any way. The physical universe is an isolated system; a closed thermos bottle is essentially an isolated system (though its insulation is not perfect).
Heat can be transferred between open systems and between closed systems, but not between isolated systems.
An intensive property is mass independent while an extensive property is one that is dependent on mass.
E.g. of intensive property –
· chemical potential
· density (or specific gravity)
· viscosity
· electrical resistivity
· spectral absorption maxima (in solution)
· specific energy
· specific heat capacity
· hardness
· melting point and boiling point
· pressure
· ductility
· elasticity
· malleability
· magnetization
· concentration
· temperature
· specific volume
E.g. of extensive property –
Energy, Entropy, Gibbs energy, Length, Mass, Particle number, Momentum, Number of moles, Volume, Electrical charge, Weight
A thermodynamic system is in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. Equilibrium means a state of balance. In a state of thermodynamic equilibrium, there are no net flows of matter or of energy, no phase changes, and no unbalanced potentials (or driving forces), within the system. A system that is in thermodynamic equilibrium experiences no changes when it is isolated from its surroundings.
In thermodynamics, a reversible process, or reversible cycle if the process is cyclic, is a process that can be "reversed" by means of infinitesimal changes in some property of the system without entropy production (i.e. dissipation of energy). Due to these infinitesimal changes, the system is in thermodynamic equilibrium throughout the entire process. Since it would take an infinite amount of time for the reversible process to finish, perfectly reversible processes are impossible.
In an irreversible process, finite changes are made; therefore the system is not at equilibrium throughout the process. At the same point in an irreversible cycle, the system will be in the same state, but the surroundings are permanently changed after each cycle.
First Law of Thermodynamics-
In our observations of the work done on, or by a gas, we have found that the amount of work depends not only on the initial and final states of the gas but also on the process, or path which produces the final state. Similarly the amount of heat transferred into, or from a gas also depends on the initial and final states and the process which produces the final state. Many observations of real gases have shown that the difference of the heat flow into the gas and the work done by the gas depends only on the initial and final states of the gas and does not depend on the process or path which produces the final state. This suggests the existence of an additional variable, called the internal energy of the gas, which depends only on the state of the gas and not on any process. The internal energy is a state variable, just like the temperature or the pressure. The first law of thermodynamics defines the internal energy (E or U) as equal to the difference of the heat transfer (Q) into a system and the work (W) done by the system.
E2 - E1 = Q – W
or
U2 – U1 = Q - W
We have emphasized the words "into" and "by" in the definition. Heat removed from a system would be assigned a negative sign in the equation. Similarly work done on the system is assigned a negative sign.
The first law of thermodynamics allows for many possible states of a system to exist, but only certain states are found to exist in nature. The second law of thermodynamics helps to explain this observation.
Relationship b/w Cp and Cv-
If a system is fully insulated from the outside environment, it is possible to have a change of state in which no heat is transferred into the system. Scientists refer to a process which does not involve heat transfer as an adiabatic process. The implementation of the first law of thermodynamics for gases introduces another useful state variable called the enthalpy.
Enthalpy which is defined to be the sum of the internal energy E or U plus the product of the pressure p and volume V. Using the symbol H for the enthalpy:
H = E + p * V
The enthalpy can be made into an intensive, or specific , variable by dividing by the mass.
Steady Flow Energy Equation-
Enthalpy is most useful for separating flow work from external work (as might be produced by a shaft crossing the control volume boundary for instance). In the figure shown below. Heat is added, a compressor is doing work on the system, the flow entering the system does work on the system (work = -p1V1), and work is done by the system through pushing out the flow (work = +p2V2). The first law relates the change in energy between states 1 and 2 to the difference between the heat added and the work done by the system. Frequently, however, we are interested only in the work that crosses the system boundary, not the volumetric or flow work. In this case it is most convenient to work with enthalpy.
This also leads to a direct physical interpretation for enthalpy. In an open flow system, enthalpy is the amount of energy that is transferred across a system boundary by a moving flow. This energy is composed of two parts: the internal energy of the fluid (u) and the flow work (pv) associated with pushing the mass of fluid across the system boundary.
Second Law of Thermodynamics-
Refrigerator
If you place your hand behind an operating refrigerator, you will notice that this area is warmer than the room temperature. Or you may notice that the refrigerator blows warm air on your feet as you stand in front of it. Yet the interior of the freezing compartment is very cold! The refrigerator is taking energy from the freezing compartment, making it colder, and exhausting that heat to the room, making it warmer.
A refrigerator is a heat engine in which work is done on a refrigerant substance in order to collect energy from a cold region and exhaust it in a higher temperature region, therby further cooling the cold region.
Refrigerators have made use of fluorinated hydrocarbons with trade names like Freon-12, Freon-22, etc. which can be forced to evaporate and then condense by successively lowering and raising the pressure. They can therefore "pump" energy from a cold region to a hotter region by extracting the heat of vaporization from the cold region and dumping it in the hotter region outside the refrigerator. The statements about refrigerators apply to air conditioners and heat pumps, which embody the same principles.
Although this process works very well and has been in place for decades, the bad news about it is that fluorinated hydrocarbons released into the atmosphere are potent agents for the destruction of the ozone in the upper atmosphere. Therefore tighter and tighter restrictions are being placed on their use.
Heat flow to a hotter region
|
Heat Pump
A heat pump is a device which applies external work to extract an amount of heat QC from a cold reservoir and delivers heat QH to a hot reservoir. A heat pump is subject to the same limitations from the second law of thermodynamics as any other heat engine and therefore a maximum efficiency can be calculated from the Carnot cycle. Heat Pumps are usually characterized by a coefficient of performance which is the number of units of energy delivered to the hot reservoir per unit work input.
Note: In calculating the coefficient of performance, or any other heat-engine related quantities, the temperatures must be the values in Kelvins.
The Carnot Cycle is one of the fundamental thermodynamic cycles and is described on this web page. We will use a p-V diagram to plot the various processes in the Carnot Cycle. The cycle begins with a gas, colored yellow on the figure, which is confined in a cylinder, colored blue. The volume of the cylinder is changed by a moving red piston, and the pressure is changed by placing weights on the piston. We have two heat sources; the red one is at a nominal 300 degrees, and the purple one is at 200 degrees. Initially, the gas is in State 1 at high temperature, high pressure, and low volume.
- The first process performed on the gas is an isothermal expansion. The 300 degree heat source is brought into contact with the cylinder, and weight is removed, which lowers the pressure in the gas. The temperature remains constant, but the volume increases. During the process from State 1 to State 2 heat is transferred from the source to the gas to maintain the temperature. We will note the heat transfer by Q1 into the gas.
- The second process performed on the gas is an adiabatic expansion. During an adiabatic process no heat is transferred to the gas. Weight is removed, which lowers the pressure in the gas. The temperature decreases and the volume increases as the gas expand to fill the volume. During the process from State 2 to State 3 no heat is transferred.
- The third process performed on the gas is an isothermal compression. The 200 degree heat source is brought into contact with the cylinder, and weight is added, which raises the pressure in the gas. The temperature remains constant, but the volume decreases. During the process from State 3 to State 4 heat is transferred from the gas to heat source to maintain the temperature. We will note the heat transfer by Q2 away from the gas.
- The fourth process performed on the gas is an adiabatic compression. Weight is added, which raises the pressure in the gas. The temperature increases and the volume decreases as the gas is compressed. During the process from State 4 to State 1 no heat is transferred.
At the end of the fourth process, the state of the gas has returned to its original state and the cycle can be repeated as often as you wish. During the cycle, work W has been produced by the gas, and the amount of work is equal to the area enclosed by the process curves. From the first law of thermodynamics, the amount of work produced is equal to the net heat transferred during the process:
W = Q1 - Q2
The Carnot Cycle has performed as an engine, converting the heat transferred to the gas during the processes into useful work.
The concept of mechanical and thermal reversibility is central to the analysis, leading to the ideal Carnot cycles. (Refer to Wikipedia:Sadi Carnot a French physicist, mathematician and engineer who gave the first successful account of heat engines, the Carnot cycle, and laid the foundations of the second law of thermodynamics).
We represent a heat engine and a heat pump cycle in a minimalist abstract format as in the following diagrams. In both cases there are two temperature reservoirs TH and TL, with TH> TL.
In the case of a heat engine heat QH is extracted from the high temperature source TH, part of that heat is converted to work W done on the surroundings, and the rest is rejected to the low temperature sink TL. The opposite occurs for a heat pump, in which work W is done on the system in order to extract heat QL from the low temperature source TL and "pump" it to the high temperature sink TH. Notice that the thickness of the line represents the amount of heat or work energy transferred.
We now present two statements of the Second Law of Thermodynamics, the first regarding a heat engine, and the second regarding a heat pump. Neither of these statements can be proved, however have never been observed to be violated.
The Kelvin-Planck Statement: It is impossible to construct a device which operates on a cycle and produces no other effect than the transfer of heat from a single body in order to produce work.
The Clausius Statement: It is impossible to construct a device which operates on a cycle and produces no other effect than the transfer of heat from a cooler body to a hotter body.
Equivalence of the Clausius and Kelvin-Planck Statements
It is remarkable that the two above statements of the Second Law are in fact equivalent. In order to demonstrate their equivalence consider the following diagram. On the left we see a heat pump which violates the Clausius statement by pumping heat QL from the low temperature reservoir to the high temperature reservoir without any work input. On the right we see a heat engine rejecting heat QL to the low temperature reservoir.
If we now connect the two devices as shown below such that the heat rejected by the heat engine QL is simply pumped back to the high temperature reservoir then there will be no need for a low temperature reservoir, resulting in a heat engine which violates the Kelvin-Planck statement by extracting heat from a single heat source and converting it directly into work.
The Clausius Theorem and Inequality
The equality above represents the Clausius Theorem and applies only the the ideal orCarnot cycle. Since the integral represents the net change in entropy in one complete cycle, it attributes a zero entropy change to the most efficient engine cycle.
The Clausius Inequality applies to any real engine cycle and implies a negative change in entropy on the cycle. That is, the entropy given to the environment during the cycle is larger than the entropy transferred to the engine by heat from the hot reservoir. In the simplified heat engine where the heat QH is all added at temperature TH, then an amount of entropy ΔS = QH/TH is added to the system and must be removed to the environment to complete the cycle. In general, the engine temperature will be less than TH for at least part of the time when heat is being added, and any temperature difference implies an irreversible process. Excess entropy is created in any irreversible process, and therefore more heat must be dumped to the cold reservoir to get rid of this entropy. This leaves less energy to do work.
Mechanical and Thermal Reversibility
Notice that the statements on the Second Law are negative statements in that they only describe what is impossible to achieve. In order to determine the maximum performance available from a heat engine or a heat pump we need to introduce the concept of Reversibilty, including both mechanical and thermal reversibility. We will attempt to clarify these concepts in terms of the following example of a reversible piston cylinder device in thermal equilibrium with the surroundings at temperature T0, and undergoing a cyclic compression/expansion process.
For mechanical reversibility we assume that the process is frictionless, however we also require that the process is a quasi-equilibrium one. In the diagram we notice that during compression the gas particles closest to the piston will be at a higher pressure than those farther away, thus the piston will be doing more compression work than it would do if we had waited for equilibrium conditions to occur after each incremental step. Similarly, thermal reversibility requires that all heat transfer is isothermal. Thus if there is an incremental rise in temperature due to compression then we need to wait until thermal equilibrium is established. During expansion the incremental fall in temperature will result in heat being transferredfrom the surroundings to the system until equilibrium is established.
In summary, there are three conditions required for reversible operation:
- All mechanical processes are frictionless.
- At each incremental step in the process thermal and pressure equilibrium conditions are established.
- All heat transfer processes are isothermal.
Carnot's Theorem
Carnot's theorem, also known as Carnot's rule, or the Carnot principle, can be stated as follows:
No heat engine operating between two heat reservoirs can be more efficient than a reversible heat engine operating between the same two reservoirs.
The simplest way to prove this theorem is to consider the scenario shown below, in which we have an irreversible engine as well as a reversible engine operating between the reservoirs TH and TL, however the irreversible heat engine has a higher efficiency than the reversible one. They both draw the same amount of heat QH from the high temperature reservoir, however the irreversible engine produces more work WI than that of the reversible engine WR.
Note that the reversible engine by its nature can operate in reverse, ie if we use some of the work output (WR) from the irreversible engine in order to drive the reversible engine then it will operate as a heat pump, transferring heat QH to the high temperature reservoir, as shown in the following diagram:
Notice that the high temperature reservoir becomes redundent, and we end up drawing a net amount of heat (QLR - QLI) from the low temperature reservoir in order to produce a net amount of work (WI - WR) - a Kelvin-Planck violator - thus proving Carnot's Theorem.
Corollary 1 of Carnot's Theorem:
The first Corollary of Carnot's theorem can be stated as follows:
All reversible heat engines operating between the same two heat reservoirs must have the same efficiency.
Thus regardless of the type of heat engine, the working fluid, or any other factor if the heat engine is reversible, then it must have the same maximum efficiency. If this is not the case then we can drive the reversible engine with the lower efficiency as a heat pump and produce a Kelvin-Planck violater as above.
Corollary 2 of Carnot's Theorem:
The second Corollary of Carnot's theorem can be stated as follows:
The efficiency of a reversible heat engine is a function only of the respective temperatures of the hot and cold reservoirs. It can be evaluated by replacing the ratio of heat transfers QL and QH by the ratio of temperatures TL and TH of the respective heat reservoirs.
Notice that we always go into "meditation mode" before replacing the ratio of heats with the ratio of absolute temperatures, which is only valid for reversible machines.
Obviously a totally impractical engine which cannot be realized in practice, since for each of the four processes in the cycle the surrounding environment needs to be changed from isothermal to adiabatic.
This engine has a piston for compression and expansion work as well as a displacer in order to shuttle the working gas between the hot and cold spaces.
________________________________________________________________________
Solved Problem 1 - Reversible Home Air Conditioner and Hot Water Heater
________________________________________________________________________
Problem 2 - A heat pump is used to meet the heating requirements of a house and maintain it at 20°C. On a day when the outdoor air temperature drops to -10°C it is estimated that the house looses heat at the rate of 10 kW. Under these conditions the actual Coefficient of Performance (COPHP) of the heat pump is 2.5.
- a) Draw a diagram representing the heat pump system showing the flow of energy and the temperatures, and determine:
- b) the actual power consumed by the heat pump [4 kW]
- c) the power that would be consumed by a reversible heat pump under these conditions [1.02 kW]
- d) the power that would be consumed by an electric resistance heater under these conditions [10 kW]
- e) Comparing the actual heat pump to the reversible heat pump determine if the performance of the actual heat pump is feasible,
Derive all equations used starting from the basic definition of COPHP.
________________________________________________________________________
Problem 3 - During an experiment conducted in senior lab at 25°C, a student measured that a Stirling cycle refrigerator that draws 250W of power has removed 1000kJ of heat from the refrigerated space maintained at -30°C. The running time of the refrigerator during the experiment was 20min. Draw a diagram representing the refrigerator system showing the flow of energy and the temperatures, and determine if these measurements are reasonable [COPR = 3.33, COPR,rev = 4.42, ratio COPR/COPR,rev = 75% > 60% - not feasible]. State the reasons for your conclusions. Derive all equations used starting from the basic definition of the Coefficient of Performance of a refrigerator (COPR).
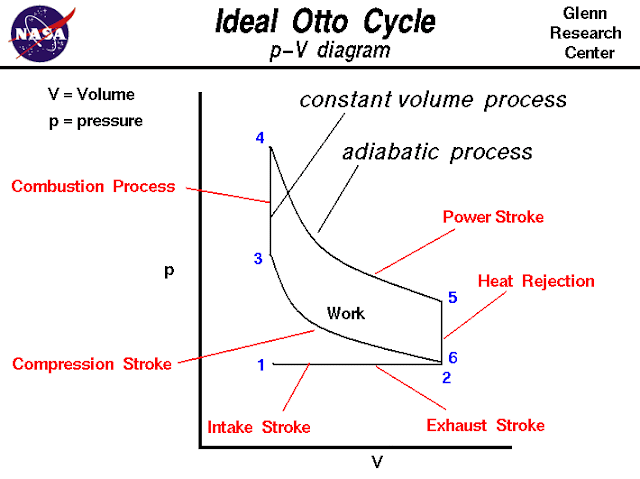
Otto Thermodynamic Cycle
On this page we discuss the Otto Thermodynamic Cycle which is used in all internal combustion engines. The figure shows a p-V diagram of the Otto cycle. Using the engine stage numbering system, we begin at the lower left with Stage 1being the beginning of the intake stroke of the engine. The pressure is near atmospheric pressure and the gas volume is at a minimum. Between Stage 1 and Stage 2 the piston is pulled out of the cylinder with the intake valve open. The pressure remains constant, and the gas volume increases as fuel/air mixture is drawn into the cylinder through the intake valve.Stage 2 begins the compression stroke of the engine with the closing of the intake valve. Between Stage 2 and Stage 3, the piston moves back into the cylinder, the gas volume decreases, and the pressure increases because work is done on the gas by the piston. Stage 3 is the beginning of the combustion of the fuel/air mixture. The combustion occurs very quickly and the volume remains constant. Heat is released during combustion which increases both the temperature and the pressure, according to the equation of state. Stage 4 begins the power stroke of the engine. Between Stage 4 and Stage 5, the piston is driven towards the crankshaft, the volume in increased, and the pressure falls as work is done by the gas on the piston. At Stage 5 the exhaust valve is opened and the residual heat in the gas is exchanged with the surroundings. The volume remains constant and the pressure adjusts back to atmospheric conditions. Stage 6 begins the stroke of the engine during which the piston moves back into the cylinder, the volume decreases and the pressure remains constant. At the end of the exhaust stroke, conditions have returned to Stage 1 and the process repeats itself.
During the cycle, work is done on the gas by the piston between stages 2 and 3. Work is done by the gas on the piston between stages 4 and 5. The difference between the work done by the gas and the work done on the gas is the area enclosed by the cycle curve and is the work produced by the cycle. The work times the rate of the cycle (cycles per second) is equal to the power produced by the engine.
Engine cycle
Idealised P/V diagram for two-stroke Otto cycle
Two-stroke
Main article: Two-stroke cycle
This system manages to pack one power stroke into every two strokes of the piston (up-down). This is achieved by exhausting and recharging the cylinder simultaneously.
The steps involved here are:
1. Intake and exhaust occur at bottom dead center. Some form of pressure is needed, either crankcase compression or super-charging.
2. Compression stroke: Fuel-air mix is compressed and ignited. In case of diesel: Air is compressed, fuel is injected and self-ignited.
3. Power stroke: Piston is pushed downward by the hot exhaust gases.
Two Stroke Spark Ignition (SI) engine:
In a two-stroke SI engine a cycle is completed in two strokes of a piston or one complete revolution (360°) of a crankshaft. In this engine the intake and exhaust strokes are eliminated and ports are used instead of valves. In this cycle, the gasoline is mixed with lubricant oil, resulting in a simpler, but more environmentally damaging system, as the excess oils do not burn and are left as a residue. As the piston proceeds downward another port is opened, the fuel/air intake port. Air/fuel/oil mixtures come from the carburetor, where it was mixed, to rest in an adjacent fuel chamber. When the piston moves further down and the cylinder doesn't have anymore gases, fuel mixture starts to flow to the combustion chamber and the second process of fuel compression starts. The design carefully considers the point that the fuel-air mixture should not mix with the exhaust, therefore the processes of fuel injection and exhausting are synchronized to avoid that concern. It should be noted that the piston has three functions in its operation:
· The piston acts as the combustion chamber with the cylinder and compresses the air/fuel mixture, receives back the liberated energy, and transfers it to the crankshaft.
· The piston motion creates a vacuum that sucks the fuel/air mixture from the carburetor and pushes it from the crankcase (adjacent chamber) to the combustion chamber.
· The sides of the piston act like the valves, covering and uncovering the intake and exhaust ports drilled into the side of the cylinder wall.
The major components of a two-stroke spark ignition engine are the:
· Cylinder: A cylindrical vessel in which a piston makes an up and down motion.
· Piston: A cylindrical component making an up and down movement in the cylinder
· Combustion chamber: A portion above the cylinder in which the combustion of the fuel-air mixture takes place
· Intake and exhaust ports: Ports that carry fresh fuel-air mixture into the combustion chamber and products of combustion away
· Crankshaft: A shaft that converts reciprocating motion of the piston into rotary motion
· Connecting rod: A rod that connects the piston to the crankshaft
· Spark plug: An ignition-source in the cylinder head that initiates the combustion process
Operation: When the piston moves from bottom dead center (BDC) to top dead center (TDC) the fresh air and fuel mixture enters the crank chamber through the intake port. The mixture enters due to the pressure difference between the crank chamber and the outer atmosphere while simultaneously the fuel-air mixture above the piston is compressed.
Ignition: With the help of a spark plug, ignition takes place at the top of the stroke. Due to the expansion of the gases the piston moves downwards covering the intake port and compressing the fuel-air mixture inside the crank chamber. When the piston is at bottom dead center, the burnt gases escape from the exhaust port.
At the time the transfer port is uncovered the compressed charge from the crank chamber enters into the combustion chamber through the transfer port. The fresh charge is deflected upwards by a hump provided on the top of the piston and removes the exhaust gases from the combustion chamber. Again the piston moves from bottom dead center to top dead center and the fuel-air mixture is compressed when the both the exhaust port and transfer ports are covered. The cycle is repeated.
Advantages: • It has no valves or camshaft mechanism, hence simplifying its mechanism and construction • For one complete revolution of the crankshaft, the engine executes one cycle—the 4-stroke executes one cycle per two crankshafts revolutions. • Less weight and easier to manufacture. • High power-to-weight ratio
Disadvantages: • The lack of lubrication system that protects the engine parts from wear. Accordingly, the 2-stroke engines have a shorter life. • 2-stroke engines do not consume fuel efficiently. • 2-stroke engines produce lots of pollution. • Sometimes part of the fuel leaks to the exhaust with the exhaust gases. In conclusion, based on the above advantages and disadvantages, two-stroke engines are supposed to operate in vehicles where the weight of the engine must be small, and it is not used continuously for long periods.
Four-stroke
Main article: Four-stroke cycle
Idealised Pressure/volume diagram of the Otto cycle showing combustion heat input Qp and waste exhaust output Qo, the power stroke is the top curved line, the bottom is the compression stroke
Engines based on the four-stroke ("Otto cycle") have one power stroke for every four strokes (up-down-up-down) and employ spark plug ignition. Combustion occurs rapidly, and during combustion the volume varies little ("constant volume").[8] They are used in cars, larger boats, some motorcycles, and many light aircraft. They are generally quieter, more efficient, and larger than their two-stroke counterparts.
The steps involved here are:
1. Intake stroke: Air and vaporized fuel are drawn in.
2. Compression stroke: Fuel vapor and air are compressed and ignited.
3. Combustion stroke: Fuel combusts and piston is pushed downwards.
4. Exhaust stroke: Exhaust is driven out. During the 1st, 2nd, and 4th stroke the piston is relying on power and the momentum generated by the other pistons. In that case, a four-cylinder engine would be less powerful than a six- or eight-cylinder engine.
There are a number of variations of these cycles, most notably the Atkinson and Miller cycles. The diesel cycle is somewhat different.
Split-cycle engines separate the four strokes of intake, compression, combustion and exhaust into two separate but paired cylinders. The first cylinder is used for intake and compression. The compressed air is then transferred through a crossover passage from the compression cylinder into the second cylinder, where combustion and exhaust occur. A split-cycle engine is really an air compressor on one side with a combustion chamber on the other.
Previous split-cycle engines have had two major problems - poor breathing (volumetric efficiency) and low thermal efficiency. However, new designs are being introduced that seek to address these problems.
The Scuderi Engine addresses the breathing problem by reducing the clearance between the piston and the cylinder head through various turbo charging techniques. The Scuderi design requires the use of outwardly opening valves that enable the piston to move very close to the cylinder head without the interference of the valves. Scuderi addresses the low thermal efficiency via firing ATDC.
Firing ATDC can be accomplished by using high-pressure air in the transfer passage to create sonic flow and high turbulence in the power cylinder.
Diesel cycle
Main article: Diesel cycle
P-v Diagram for the Ideal Diesel cycle. The cycle follows the numbers 1-4 in clockwise direction.
Most truck and automotive diesel engines use a cycle reminiscent of a four-stroke cycle, but with a compression heating ignition system, rather than needing a separate ignition system. This variation is called the diesel cycle. In the diesel cycle, diesel fuel is injected directly into the cylinder so that combustion occurs at constant pressure, as the piston moves.
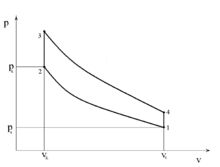
Otto cycle: Otto cycle is the typical cycle for most of the cars internal combustion engines, that work using gasoline as a fuel. Otto cycle is exactly the same one that was described for the four-stroke engine. It consists of the same four major steps: Intake, compression, ignition and exhaust.
PV diagram for Otto cycle On the PV-diagram, 1-2: Intake: suction stroke 2-3: Isentropic Compression stroke 3-4: Heat addition stroke 4-5: Exhaust stroke (Isentropic expansion) 5-2: Heat rejection The distance between points 1-2 is the stroke of the engine. By dividing V2/V1, we get: r
where r is called the compression ratio of the engine.
Rankine cycle
The Rankine cycle is a mathematical model that is used to predict the performance of steam engines. The Rankine cycle is an idealised thermodynamic cycle of a heat engine that converts heat into mechanical work. The heat is supplied externally to a closed loop, which usually uses water as the working fluid. The Rankine cycle, in the form of steam engines generates about 90% of all electric power used throughout the world.
The Rankine cycle most closely describes the process by which steam-operated heat engines most commonly found in power generation plants generate power. The two most common heating processes used in these power plants are nuclear fission and the combustion of fossil fuels such as coal, natural gas, and oil.
The Rankine cycle is sometimes referred to as a practical Carnot cycle because, when an efficient turbine is used, the TS diagram begins to resemble the Carnot cycle. The main difference is that heat addition (in the boiler) and rejection (in the condenser) are isobaric in the Rankine cycle and isothermal in the theoretical Carnot cycle. A pump is used to pressurize the working fluid received from the condenser as a liquid instead of as a gas. All of the energy in pumping the working fluid through the complete cycle is lost, as is most of the energy of vaporization of the working fluid in the boiler. The vaporization energy is rejected from the cycle through the condenser. But pumping the working fluid through the cycle as a liquid requires a very small fraction of the energy needed to transport it as compared to compressing the working fluid as a gas in a compressor (as in the Carnot cycle).
The efficiency of a Rankine cycle is usually limited by the working fluid. Without the pressure reaching super critical levels for the working fluid, the temperature range the cycle can operate over is quite small: turbine entry temperatures are typically 565°C (the creep limit of stainless steel) and condenser temperatures are around 30°C. This gives a theoretical Carnot efficiency of about 63% compared with an actual efficiency of 42% for a modern coal-fired power station. This low turbine entry temperature (compared with a gas turbine) is why the Rankine cycle is often used as a bottoming cycle in combined-cycle gas turbine power stations.
Description:
The working fluid in a Rankine cycle follows a closed loop and is reused constantly. The water vapor with condensed droplets often seen billowing from power stations is generated by the cooling systems (not from the closed-loop Rankine power cycle) and represents the means for low quality (low temperature) heat to exit the system, making room for the re-addition of new high quality heat that can be converted to useful work. This exhaust heat is represented by the "Qout" flowing out the bottom of the Ts cycle in the diagram below. Note that cooling towers operate using the latent heat of vaporization of the cooling fluid. While many substances could be used in the Rankine cycle, water is usually the fluid of choice due to its favorable properties, such as nontoxic and nonreactive chemistry, abundance, and low cost, as well as its thermodynamic properties.
One of the principal advantages the Rankine cycle holds over others is that during the compression stage relatively little work is required to drive the pump, the working fluid being in its liquid phase at this point. By condensing the fluid, the work required by the pump consumes only 1% to 3% of the turbine power and contributes to a much higher efficiency for a real cycle. The benefit of this is lost somewhat due to the lower heat addition temperature. Gas turbines, for instance, have turbine entry temperatures approaching 1500°C. Nonetheless, the efficiencies of actual large steam cycles and large modern gas turbines are fairly well matched.
The four processes in the Rankine cycle:
There are four processes in the Rankine cycle. These states are identified by numbers (in brown) in the above Ts diagram.
Process 1-2: The working fluid is pumped from low to high pressure. As the fluid is a liquid at this stage the pump requires little input energy.
Process 2-3: The high pressure liquid enters a boiler where it is heated at constant pressure by an external heat source to become a dry saturated vapor. The input energy required can be easily calculated using mollier diagram or h-s chart or enthalpy-entropy chart also known as steam tables.
Process 3-4: The dry saturated vapor expands through a turbine, generating power. This decreases the temperature and pressure of the vapor, and some condensation may occur. The output in this process can be easily calculated using the Enthalpy-entropy chart or the steam tables.
Process 4-1: The wet vapor then enters a condenser where it is condensed at a constant pressure to become a saturated liquid.
In an ideal Rankine cycle the pump and turbine would be isentropic, i.e., the pump and turbine would generate no entropy and hence maximize the net work output. Processes 1-2 and 3-4 would be represented by vertical lines on the T-S diagram and more closely resemble that of the Carnot cycle. The Rankine cycle shown here prevents the vapor ending up in the superheat region after the expansion in the turbine, [1] which reduces the energy removed by the condensers.

























No comments:
Post a Comment